Применение методов обнаружения и компенсации ошибок в целочисленном
классе cBigNumber
Р.Н. Шакиров
Институт машиноведения УрО РАН
raul@imach.uran.ru
Данный текст является препринтом публикации в журнале "Программирование" (С) Р.Н.Шакиров, 2010
www.naukaran.ru
Обсуждается практика использования автоматических методов обнаружения и компенсации ошибок в классе cBigNumber, написанном на языке C++ для выполнения операции над неограниченными целыми числами. Класс реализует штатные операции языка C++, извлечение квадратного корня, возведение в степень по модулю и проверку на простоту по методу Миллера-Рабина. Тестирование класса проведено в автоматическом режиме. Достоверность вычислений обеспечивается встроенными средствами контроля и компенсации ошибок.
Ключевые слова: контроль ошибок, компенсация ошибок, автоматическое тестирование, C++
Введение
Ошибки в программах являются данностью, которая должна учитываться при любых способах применения вычислительной техники. Современная технология программирования настолько способствует их возникновению, что отсутствие сведений об ошибках следует считать плохим признаком – скорее всего, программа еще не доведена до практического применения, и только поэтому содержащиеся в ней ошибки еще не выявлены. Наоборот, хорошим признаком является большое число обнаруженных и исправленных ошибок, а также применение автоматических методов отладки и тестирования, которые более эффективны, чем ручные методы.
В этой статье речь пойдет об арифметических ошибках, которые до сих пор считаются из ряда вон выходящим явлением – хотя они так же закономерны, как и ошибки любых других разновидностей. Разница заключается разве в том, что арифметические ошибки нельзя списать на «особенности реализации». Поэтому вполне возможно, что именно с арифметики начнется создание безошибочных программ, сейчас же нам остается просто наблюдать за процессом совершения, выявления и предотвращения ошибок — чем мы здесь и будем заниматься.
Объектом исследования послужат операции над неограниченными целыми числами. Эта популярная задача одновременно проста и парадоксально сложна. Предлагаемые решения могут в тысячи раз отличаться по производительности, часто имеют скрытые ошибки и требуют для правильной работы выполнения множества явных и неявно подразумеваемых условий.
1. О понятии ошибки
Слово «ошибка» имеет большое число различных значений. В этот статье под ошибкой понимается ситуация, когда какая-либо часть кода программы ведет себя не так, как ожидает программист («сделать хотел утюг – слон получился вдруг») — т.е. во всем жизненном цикле программы мы рассматриваем исключительно процессы написания и тестирования кода. В частности, не рассматриваются ошибки при постановке задачи. Но учитываются ошибки в алгоритмах, если алгоритмы создавались в процессе написания кода и отлаживались вместе с ним.
Ошибки возникают в силу внешних факторов (непредсказуемый сбой в аппаратуре, операционной системе, промежуточном программном обеспечении или трансляторе) и по недосмотру программиста. Факторы возникновения ошибок будут рассмотрены в следующих разделах. А по своим последствиям ошибки будут разделены на три основные категории:
1. Фатальная ошибка – при ее возникновении программа прекращает работу. Фатальные ошибки весьма неприятны, но полностью исключить их нельзя – даже если код программы безупречен, они всегда могут произойти по внешним причинам.
2.
Компенсированная
ошибка – возникает, но затем происходит ее компенсация, благодаря которой программа
продолжает работу и даже выдает правильный результат. Обнаружить такую ошибку
можно при тестировании кода программы по частям. Механизм компенсации может
быть встроен в программу целенаправленно, для нейтрализации ошибок определенного
класса или возникнуть стихийным путем. В последнем случае нет уверенности в том,
что компенсация всегда сработает надлежащим образом, т.е. речь может идти о
т.н. «скрытой» ошибке.
3.
Арифметическая
ошибка – программа продолжает работу и выдает результат, который всегда или
при определенных условиях оказывается неверным. Арифметические ошибки надо
устранить, а если это не удается сделать полностью – то перевести их в
категорию компенсированных или фатальных ошибок.
2. О влиянии ошибок в аппаратуре и системном программном обеспечении
Разработчики программ часто предполагают, что аппаратура и операционная система компьютера работают безошибочно. Более правильное утверждение состоит в том, что ошибки в платформе относительно редки по сравнению с ошибками в прикладных программах. Но раз мы стремимся свести число ошибок к минимуму, то следует учитывать все их возможные источники.
1. Нештатный режим работы. Производитель аппаратуры готовит ее к работе в штатном режиме, но требуемые им условия работы не всегда соблюдаются. На некоторых компьютерах уже через полгода-год работы отказывают вентиляторы системы охлаждения, другие могут собираться из перемаркированных комплектующих. Нештатные условия работы не всегда приводят к отказу техники. Поскольку каждый вычислительный блок имеет индивидуальный запас стабильности, то бывают случаи, когда при сохранении общей работоспособности компьютера в отдельных его блоках происходят периодические сбои, частота которых зависит от величины перегрева, «разгона», деградации кристалла, радиационного фона и других нештатных факторов.
К примеру, ошибки в блоке вычислений с плавающей точкой (FPU — floating point unit) могут остаться незамеченными, т.к. FPU не является принципиальным для устойчивой работы операционной системы. Поэтому известная программа поиска простых чисел Prime95 [1] перед проведением расчетов тестирует FPU. Тестирование позволяет убедиться в первоначальной работоспособности FPU, но не гарантирует его дальнейшую правильную работу, если, к примеру, изменится первоначальный тепловой режим. В классе cBigNumber принят другой подход — используется только основное целочисленное ALU. Это ключевой вычислительный блок, т.к. периодические сбои в «быстрых» операциях сложения/вычитания/сдвига, логике и адресной арифметике приводят к краху операционной системы (как только сбои придутся на квант времени, в котором выполняется операционная система — обычно это дело нескольких миллисекунд, немного больше на многоядерных и многопроцессорных компьютерах, где операционная система по очереди выполняется на всех вычислительных ядрах). Поэтому мы полагаем, что если компьютер работает, то все «быстрые» операции целочисленного ALU выполняются правильно. Уточним, что речь идет о 32-разрядных операциях, т.к. 64-разрядная арифметика не нагружается операционной системой по всей разрядной сетке. Более высока устойчивость операционной системы и по отношению к сбоям целочисленного умножения и деления, т.к. эти «медленные» операции реже задействуются системными программистами.
2. Случайные сбои. Кроме периодических сбоев, вызванных нештатными
режимами работы, в компьютерах могут происходить случайные аппаратные сбои.
Надо отметить, что любые способы компенсации сбоев не дают полной гарантии восстановления
данных, хотя вероятность ошибки по известной теореме Шеннона можно сделать
сколь угодно малой. Поэтому мы будем полагаться на то, что последствия
случайных сбоев в достаточной степени исправляются схемами аппаратного контроля,
которые собственно для этого и предназначены. В частности, современные микропроцессоры
Intel и AMD имеют надежное целочисленное ядро и
защищают подсистему памяти контролем четности в кэше
1-го уровня и кодами коррекции ошибок (ECC) в кэшах
2-го и 3-го уровней. А внешняя оперативная память может иметь или не иметь ECC – в нашем случае требуется, чтобы она его имела. Это
значит, что для расчетов надо
использовать компьютеры класса не ниже рабочей станции, техника бытового и
офисного типа для этой цели не подходит.
3. Экспериментальные
технологии. Новый класс аппаратных сбоев связан с многоядерными
процессорами. Вот две ошибки из Errata к процессорам
Core 2 Duo [2]:
AI39 Запрос
кэш-линейки L1-кэша разрушает модифицированную кэш-линейку другого ядра.
AI43 Параллельные
записи в "чистые" страницы памяти на многопроцессорных системах ведут
к неопределенному поведению.
Что и говорить — процессор хороший
и быстрый, вот только вычислять на нем нельзя! Указанные ошибки могут проводить
к случайному искажению данных. Правда, Errata
указывает, что ошибки компенсируются путем обновления BIOS (которое,
по-видимому, загружает в процессор обновленный микрокод). Остается проверить,
сделано ли это в обновлении BIOS к расчетному компьютеру. Тео де Раадт, обративший внимание на эти и другие ошибки,
советовал подождать год, пока разработчики Core 2 Duo их не исправят. С тех пор
число обнаруженных, но не исправленных ошибок в Core 2 Duo выросло в два раза,
а Intel выпускает следующее поколение многоядерных
микропроцессоров Core i7.
Среди разработчиков операционных
систем более надежными считаются микропроцессоры предыдущего поколения —
Intel Pentium 4 и AMD Athlon 64. Но и здесь встречаются свои ошибки — мы наблюдали
порчу памяти на Athlon 64 X2 при работающей виртуальной машине VirtualBox. Поэтому в ответственных случаях лучше отказаться от виртуальности, многоядерности
и других новых недоотлаженных технологий.
4. Переносимость или непереносимость? Проблема переносимости существует и в такой хорошо изученной области, как математические вычисления. Самый известный пакет для работы с большими числами – GMP принципиально ориентирован на UNIX-платформы, причем даже при таком существенном ограничении его разработчики пожаловались на то, что они с 1996 года нашли около 100 ошибок, связанных с применением различных трансляторов: «We are seeing ever increasing problems with miscompilations of the GMP code... Thus far, we've found on-the-order-of 100 compiler bugs.» [3]. Вопросы использования GMP на платформе Windows освещаются на сайте [4].
Чтобы сократить ошибки при использовании вычислительных пакетов, следует по возможности применять «авторский» транслятор и вид микропроцессора – для большинства известных пакетов больших чисел это UNIX на x386. В отличие от этой практики, класс cBigNumber тестируется и отлаживается на популярной платформе Windows под 32-разрядным транслятором Microsoft Visual C++, а компиляция на других платформах обеспечивается соблюдением стандарта C++ ISO/IEC 14882:1998(E). Основные тестовые микропроцессоры - Intel Pentium 4 и AMD Athlon 64.
5. Обоснование выбора алгоритмов. Алгоритмы часто сравнивают по производительности получаемых из них программ. Но вопрос о высокой производительности (в нашем случае – скорости выполнения математических операций) уместно ставить только в том случае, если все операции выполняются математически корректно – иначе получится соревнование на скорость получения неверного результата. Поэтому от алгоритмов мы требуем – 1) устойчивости по отношению к ошибкам аппаратуры, и 2) производительности, поскольку при уменьшении времени расчетов сокращается вероятность аппаратной ошибки.
По этим критериям нами выбраны «школьные» алгоритмы выполнения арифметических операций в дополнительном двоичном коде. Они задействуют только целочисленное ALU, причем вместо аппаратного умножения и деления можно эффективно использовать последовательные сложения/вычитания – это важно на микропроцессоре Pentium 4, где целочисленное умножение и деление выполняются через ненадежный блок FPU. Иначе устроены микропроцессоры Athlon/Phenom и Core – целочисленное умножение выполняется в целочисленном ALU, т.е. а) более достоверно и б) значительно быстрее — рост производительности по сравнению с аддитивным методом составляет до 700%. Такой рост производительности оправдывает риск, связанный с применением блока аппаратного умножения — поэтому в классе cBigNumber предусмотрены оба способа выполнения умножения, каждый из которых оптимален для своего вида микропроцессора.
Для дополнительного увеличения производительности применяется блочный метод умножения Карацубы [5], деление с таблицей сдвигов и некоторые другие методы, не слишком далеко отходящие от «школьной» методологии (полезно отметить, что метод Карацубы иногда рекомендуют для изучения в школе). Как более сложные, эти методы могут быть источниками дополнительных ошибок в коде класса (см. раздел 6), поэтому они могут быть отключены в пользу более простых методик. Обоснованность их применения определяется увеличением производительности, которое наблюдается при операциях над числами размером от нескольких тысяч бит и выше.
Считается, что «школьные» методы
дают наилучшую производительность при размере чисел до 10-20 тысяч бит, а
дальше выигрывает более сложная математика, начиная с методов на основе
применения FFT, которые явным образом задействуют блок FPU. Но результаты сравнения в очень сильной степени
зависят от применяемого аппаратного обеспечения и особенностей программного
кода. По данным нашего внутреннего сравнения на микропроцессорах AMD, метод
умножения Карацубы оказывается быстрее метода FFT при размере числа до 100
тысяч бит и выше.
Для справки в табл. 1 даны
результаты выполнения основных тестов на различных микропроцессорах. Вычисления
проводятся в одном потоке. В колонках asm
приведены результаты оптимизированного кода, использующего встроенный ассемблер
x386 для 32-разрядных трансляторов Microsoft Visual C++ и Borland
C++ Builder. Для сравнения в колонках C++ приведены результаты
машинно-независимого кода на языке C++, а в колонках NTL – результаты известной
библиотеки неограниченных чисел [6], которая использует схожую с нашей алгоритмическую
базу. Под Windows библиотека NTL не использует
машинно-зависимые операции, вместо этого проводится глубокая оптимизация C кода с применением FPU. Эта оптимизация дает хороший
эффект на микропроцессорах Pentium 4, для которых она, по-видимому, и
проводились. В отличие от NTL, класс cBigNumber показывает наилучшую
производительность на процессорах AMD (Athlon и Phenom).
Тест Умножение Деление Возведение в степень
(размер операндов ~250000 и
~65000 бит) 65907856907890 по
~25000 битному модулю
Процессор asm NTL
C++ asm NTL
C++ asm NTL
C++
-----------------------------------------------------------------------------
Atom
N270 33 109 366
570 561
1242 2235 1859 5969
Pentium
III/933 55 214 494
970 1056
2005 2906 3494 8578
Pentium 4C/2400 45 64
245 611 278 981
2343 906
4297
Athlon
900 29 135
469 543
705 1729
1892 2123 8051
Athlon
XP 2500+ 14 66
230 263
345 900 906 1047 4094
Athlon
64 X2 3800+ 11 56 175 236
298 697 813 969 3172
Phenom II X3 710
8 44
133 161 233 479
603 834 2380
Core
Duo T2500 28 70 217
359 241 786 1437
844 3765
Core 2 Duo E6420 23 70
175 313 205 606
1234 735 2937
Табл.
1. Время выполнения однопоточных тестов в мс.
3. Предотвращение ошибок при использовании класса
Методы, помогающие человеку не совершать ошибки, в инженерной практике почему-то называются «защитой от дурака». Но не будем обижаться — пусть разработчики называют нас как угодно, лишь бы их программы терпеливо относилась к нашим ошибкам. Иной распространенный вариант — т.н. «неопределенное поведение» нас не устраивает.
В классе cBigNumber защита от человеческих ошибок основана на строгом выполнении спецификации С++. Т.е. арифметические действия выполняются операторами + - * / %, сдвиги операторами <<, >>, битовые маски применяются операторами & | и ^. Можно использовать все постфиксные, префиксные и бинарные операторы накопления. Потоковый ввод-вывод работает также, как в С++, со всеми модификаторами. В том числе работает установка основания cin >> dec, помогающая избавиться от известной ошибки при вводе оператором чисел, начинающихся с нуля — многие программы на C++ воспринимают эти числа, как восьмеричные данные.
Можно написать и отладить программу для работы с штатными целыми числами, а затем перевести ее на неограниченные числа простой заменой деклараций на cBigNumber, как на примере 1.
#include "Cbignum.h"
#include "Cbignums.h"
#include <fstream.h>
#define DIM 3
void main (int argc, char **argv)
{
cBigNumber m1 [DIM] [DIM], m2 [DIM] [DIM], m3 [DIM]
[DIM];
int i,
j, k;
ifstream fin (argv
[1]);
fin >> dec;
for (i = 0; i
< DIM; i++) for (j = 0; j < DIM; j++) fin
>> m1 [i] [j];
for (i = 0; i
< DIM; i++) for (j = 0; j < DIM; j++) fin
>> m2 [i] [j];
for (i = 0; i
< DIM; i++) {
for (j = 0; j < DIM; j++){
cBigNumber sum = 0;
for (k = 0; k < DIM; k++) sum += m1 [i]
[k] * m2 [k] [j];
m3 [i] [j] = sum;
}
}
ofstream fout
(argv [2]);
for (i = 0; i
< DIM; i++) {
for (j = 0; j < DIM; j++) fout
<< m3 [i] [j] << " ";
fout << '\n';
}
}
Пример 1. Программа перемножения квадратных матриц 3x3.
По стандарту C++ выполняются комбинированные операции над числами cBigNumber, long, int и short с приведением к большему типу cBigNumber. Но надо остерегаться беззнаковых чисел — они перед комбинированной операцией сначала приводятся к типу long, при этом старший значащий бит становится знаковым. Как нетрудно догадаться, это отступление от стандарта становится источником ошибок, т.к. программист ожидает приведения беззнакового числа непосредственно к большему типу cBigNumber. К сожалению, попытка исправить ситуацию приводит к разбуханию заголовочных файлов и появлению проблем совместимости со старыми трансляторами.
Другое отличие связано с тем, что объекты cBigNumber при объявлении устанавливаются в 0, если их начальное значение не указано, в то время как штатные автоматические переменные и массивы C++ получают пресловутые «неопределенные значения». Обнуление не может считаться отступлением от спецификации, т.к. 0 является частным случаем «неопределенного значения».
Специальные функции — cBigPow, cBigPowMod и cBigSqrt и другие применяются для тех операций, которых нет в языке C++.
4. Автоматическое распределение памяти
Раз мы следуем соглашениям C++, то прикладной программист не должен сам распределять память под объекты класса cBigNumber. Вместо этого, распределение выполняется автоматически с помощью разработанных нами шаблонов динамических массивов [7,8], реализующих известный метод резервирования памяти.
Конструктор класса создает объект
с нулевым значением без выделения динамической памяти (это позволяет создавать
разреженные массивы из неограниченных чисел при минимальном расходе памяти).
Память выделяется при первом присваивании с учетом возможности дальнейшего
увеличения числа. В среднем, резервируется около трети от необходимого объема
памяти; если этой памяти в дальнейшем не хватит, то проводится повторное резервирование.
Минимальное количество слов, отводимых под число – около 25. При уменьшении
числа вся высвобожденная память остается в резерве. При описанном способе
выделения памяти общее число операций распределений памяти пропорционально логарифму
максимального размера памяти в машинных словах.
Высвобождение памяти выполняется в
деструкторе класса, который автоматически удаляет объект класса при выходе из
области видимости. Но если объект класса создавался неявным образом для
хранения результата операции, то он остается в памяти в качестве буфера для результата
последующих операций.
Как показывает практика, редкий
прикладной программист может реализовать более эффективный способ распределения
памяти (хотя такое возможно для каждой конкретной задачи). В основном,
программисты заказывают максимально необходимый объем памяти, а если его
все-таки не хватает — то возникает всем известная ошибка «переполнения буфера».
Поскольку класс не
ограничивает величину чисел, то для их хранения могут потребоваться массивы
любого размера. Поэтому шаблоны отслеживают ситуацию переполнения системной разрядной
сетки. В этом случае, а также при исчерпании доступного адресного пространства
или виртуальной памяти они завершают работу программы вызовом системной функции
abort.
Шаблоны могут применяться для создания многомерных неограниченных массивов из любых объектов, в том числе объектов класса cBigNumber, как это проиллюстрировано на примере 2.
#include "Cbignum.h"
#include "Cbignums.h"
#include <fstream.h>
void main (int argc, char **argv)
{
typedef exarray<cBigNumber> row;
exarray <row> m1,m2,m3;
int i,
j, k, dim
ifstream fin (argv
[1]);
fin >> dec >> dim;
for (i = 0; i
< dim; i++) for (j = 0; j < dim; j++) fin
>> m1 [i] [j];
for (i = 0; i
< dim; i++) for (j = 0; j < dim; j++) fin
>> m2 [i] [j];
for (i = 0; i
< dim; i++) {
for (j = 0; j < dim; j++){
cBigNumber sum = 0;
for (k = 0; k < dim; k++) sum += m1 [i]
[k] * m2 [k] [j];
m3 [i] [j] = sum;
}
}
ofstream fout
(argv [2]);
for (i = 0; i
< dim; i++) {
for (j = 0; j < dim; j++) fout
<< m3 [i] [j] << " ";
fout << '\n';
}
}
Пример 2. Программа перемножения неограниченных квадратных матриц.
5. Встроенные средства контроля и коррекции ошибок
Язык С++ сам по себе мало подходит для разработки надежных программ, но он достаточно гибок для того, чтобы соответствующие средства можно было реализовать путем его расширения.
Разработанные нами шаблоны динамических массивов обеспечивают два режима распределения памяти – автоматический для массивов неограниченного размера [7] и ручной со страховкой [8], когда программист задает требуемые размеры массива, а программа в процессе выполнения автоматически отслеживает ошибки выхода индекса за границу массива.
По соображениям производительности, в арифметическом ядре класса cBigNumber применяется ручное распределение памяти. В этом случае возможны ошибки распределения памяти, из-за которых в определенных ситуациях будут возникать ошибки индексации, более известные как ошибки «переполнения буфера» Но потенциально неверный результат получен не будет, т.к. при ошибке индексации программа завершит работу с выдачей диагностики.
Для увеличения производительности предусмотрена возможность отключения контроля индексов — везде или только на критических по времени участках кода, при этом в конец массива автоматически добавляется как минимум один дополнительный страховочный элемент. Данная страховка не равноценна контролю индексов, но она компенсирует один распространенный класс ошибок – обращение к элементу, следующему за последним в массиве.
Применение контроля индексов в классе cBigNumber проиллюстрировано на примере 3.
class cBigNumber: public exblock<long>
// Класс cBigNumber объявляется как производный
от динамического
// массива типа long. Его элементы мы будем
назвать словами.
// В нулевое слово массива записывается число
слов, требуемых
// для двоичного дополнительного кода
неограниченного числа,
// далее сам код.
{
...
// Оператор
присваивания неограниченного числа
cBigNumber& operator = (const
cBigNumber& b)
{
checkexpand (b.length());
//
Распределение памяти под заданное число слов.
// Метод length()
сообщает число long слов в двоичном коде b,
// т.е. b[0]. Это же
число передается в checkexpand(), т.к.
// при копировании число слов не меняется.
//
Метод checkexpand() подстраивает размер
массива до заданного
// максимального индекса (т.е. если задан индекс
n, то число
// элементов будет n +
1). Если контроль индексов отключен,
//
то выделяется, как минимум, один резервный элемент.
CbigNumberCopy (EXPTRTYPE(b),
EXPTRTYPE(*this));
// Копирование неограниченного числа b в *this.
// В режиме с контролем индекса макросы
EXPTRTYPE подставляются как
// (b,
*this)
// В режиме без контроля индексов макросы
EXPTRTYPE подставляются как
// (b.base(),
this->base())
//
Метод base() выдает указатель на базовый С массив.
return *this;
}
...
}
void
cBigNumberCopy (const EXPTR(long) p1, EXPTR(long)
p)
// Функция копирования.
// В режиме с контролем индекса макросы EXPTR
подставляются как
//
(const exptr<long> p1, exptr<long> p)
// В режиме без контроля индекса макросы EXPTR
подставляются как
// (const *p1, const *p)
// Объект exptr<>
работает аналогично обычному указателю C, но
// дополнительно содержит информацию о размере
массива для контроля
// индексов, который
проводится при каждом обращении к массиву.
// Если в методе класса мы распределим
недостаточное число слов,
//
то здесь эта ошибка будет обнаружена.
{
size_t n1 = (size_t)(*p++ = *p1++);
if (n1) do { *p++
= *p1++; } while (--n1 != 0);
}
Пример 3. Реализация оператора присваивания в классе cBigNumber
Другой применяемый нами метод динамического контроля заключается в проверке предусловий и постусловий операций во внешних и внутренних методах класса. В качестве примера предусловия можно привести проверку деления на 0, а в постусловии обычно проверяется знак результата операции, т.к. ошибки при вычислениях в дополнительном коде довольно часто приводят к его искажению.
6. Организация и результаты тестирования класса cBigNumber
На первый взгляд, тестирование класса неограниченных целых чисел представляется достаточно простой задачей. Математика есть только в методе Миллера-Рабина и алгоритме квадратного корня, остальное – арифметика на «школьных» алгоритмах, которые просты и очевидны. При этом операции всегда выполняются точно, т.е. нет проблем округления и редукции, которые доставляют неприятности при выполнении операции с плавающей точкой [10]. И даже величина чисел не ограничена, поэтому — с математической точки зрения — единственным особым значением является 0. Другое дело, что операции над очень большими числами могут потребовать очень много времени — но в существующей версии класса эта проблема пока не учитывается. Что же остается делать в таких тепличных условиях? Протестировать арифметику с помощью генератора примеров и отдельно проверить реализацию следующих особых ситуаций:
1. Деление на 0 и остаток от деления на 0. Класс выполняет целочисленное деление на 0, чтобы вызвать соответствующую реакцию транслятора, поскольку по стандарту ISO/IEC 14882:1998(E) «the behavior is undefined». Если ничего не происходит, то выдается частное 0 и остаток, равный делимому. При необходимости, неопределенную реакцию C++ можно заблокировать и ограничиться штатной установкой класса.
2. Возведение степень по модулю 0. Аналогично делению на 0, но если программа не завершается, то выдается 1.
3. Возведение в степень 0 (выдается 1) и в отрицательную степень (1/основание возводится в положительную степень).
4. Сдвиги на 0 бит (значение не изменяется) и на отрицательное число бит (стандарт это не оговаривает, поэтому меняем направление сдвига).
5. Квадратный корень из отрицательного числа (выдается 0).
6.1. О неэффективности тестирования по спецификации
Описанное выше тестирование, которое проверяет только спецификацию класса, не будет эффективным. Есть, по крайней мере, две группы ошибок, которые им не обнаруживаются:
1) Многочисленные граничные значения возникают внутри самого класса из-за того, что мы не везде пользуемся неограниченной арифметикой. К примеру, подсчет числа значащих бит в числах, который нужен в некоторых алгоритмах, проводится с использованием переменных типа long, которые подвержены переполнению разрядной сетки. Индексы типа size_t используются при обращении к внутреннему представлению чисел. При этом они имеют, как минимум, восьмикратный запас до максимально возможного значения — и каждое индексное выражение надо проверять на то, чтобы этого запаса хватило для представления всех промежуточных результатов.
Для тестирования переполнения разрядной сетки надо создавать очень большие примеры с миллиардами значащих бит, которые на практике не актуальны из-за неприемлемо большого времени счета. Поэтому вместо тестирования переполнения мы ограничились ручным анализом кода, которое впоследствии может быть дополнено формальной верификацией (см. раздел 7).
2) Самые трудные для поиска и наиболее актуальные на практике ошибки возникают оттого, что мы отказались от полностью автоматического распределения памяти [7] и, вместо этого, вычисляем требуемые размеры массивов по формулам. Рассмотрим наш ранний пример, относящийся к 2003 году [9].
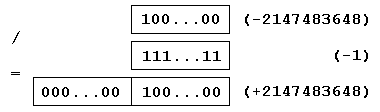
Рис. 1. Пример
деления (старшие слова и биты слева)
При делении целых чисел в двоичном дополнительном коде частное может занимать на 1 слово больше, чем делимое (рис. 1). А если по ошибке распределить для частного такое же количество слов, что и для делимого, то знак результата будет неверным (-2147483648). Отметим, что во всех других примерах 32-разрядного деления лишнее слово не потребуется и ошибка не произойдет.
Предположим теперь, что в программе деления есть указанная ошибка распределения памяти и оценим вероятность ее обнаружения при автоматическом тестировании на случайных парах 32-разрядных чисел. Вероятность получить указанную в примере пару чисел равна (1/232)2 = 1/264. При проверке миллиарда пар в секунду математическое ожидание времени обнаружения ошибки будет 264 / (2 * 109 * 3600 * 24 * 365.25) » 292 года.
Приведенный пример иллюстрирует невозможность выявления всех арифметических ошибок при тестировании на случайно подобранных примерах. При таком тестировании отлавливаются только «наиболее вероятные» ошибки, а «наименее вероятные» остаются вне поля зрения.
6.2. Наша методика тестирования класса
Чтобы генератор примеров чаще выдавал потенциально проблемные комбинации, мы поправили случайное распределение в пользу чисел, которые могут быть источниками ошибок. При генерации каждого операнда случайным образом выбирается: знак, число значащих шестнадцатеричных цифр (от 1 до 9999) и число дополнительных младших нулей (от 0 до 40). Число значащих шестнадцатеричных цифр выбирается так, чтобы с примерно одинаковой вероятностью появлялись числа с 1..9, 10..99, 100…999 и 1000...9999 значащими цифрами. Дополнительно, примерно до 1/40 увеличена вероятность появления чисел всего с одним значащим битом, подобных числам на рис. 1. После определения характеристик операнда его значащая часть заполняется с помощью 3-tausworth псевдослучайного генератора.
Для тестирования созданы программы Arifexp и Miller:
1) Программа Arifexp автоматически строит примеры, проводит операции с длинными числами и проверяет результат по методам обратной и альтернативной прямой операции (большинство операций реализовано в классе несколькими различными способами, поэтому можно проводить проверку по методу независимых алгоритмов, см. раздел 8). Особый способ предусмотрен для проверки внутреннего распределения памяти в алгоритме умножения — проверочное умножение выполняется по неоптимальной схеме, когда первый операнд короче второго (штатное умножение в этом случае меняет операнды местами). Эта проверка задействует труднодостижимые режимы распределения памяти в методе Карацубы, благодаря чему программа Arifexp за две недели счета нашла арифметическую ошибку 2007.A4 (см. ниже), которая в ином случае вообще не была бы обнаружена. Остальные ошибки были выявлены быстрее — за несколько дней счета.
2) Программа Miller проверяет на простоту нечетные числа малой разрядности — по методу Миллера-Рабина [11] и путем факторизации, результаты двух разных методов проверки сравниваются.
Понятно, что наши программы тестирования не гарантируют выявление всех ошибок. Разработчики не знают заранее все случаи, в которых они могут ошибиться. Но с помощью тестирования можно оценить эффективность принятых мер по сокращению числа ошибок — для чего сравнивается число ошибок, обнаруженных автоматическими и ручными методами.
6.3. Результаты
тестирования класса
К настоящему времени программа Arifexp протестировала класс на более чем 10 миллиардах псевдослучайных примеров с разрядностью от 1 до 12,000,000 бит. Программа Miller проверила на простоту более миллиарда числа малой разрядности.
Автоматическому тестированию подвергается математическое ядро класса и методы ввода-вывода. Тестирование проводится непрерывно, при этом проверяются все задействованные операции, даже если в них больше не обнаруживаются ошибки. Далее мы будем обсуждать результаты тестирования математического ядра класса (7800 строк кода С++ с комментариями). Меньшая по размеру и значению подсистема ввода-вывода обсуждалась ранее в работе [9].
Встроенными средствами контроля и коррекции (см. раздел 5) обнаружено 12 ошибок:
2003.1-5 Переполнение буфера в отладочном режиме методов addmul, tab, addmultab, умножения и деления.
2003.7A При делении может быть получено частное с неверным знаком.
2003.8U Переполнение буфера в методе powmod.
2005.9U Переполнение буфера при возведении в степень по отрицательному модулю со старшим словом 0x80000000.
2005.10U Переполнение буфера при возведении в степень по модулю 0, если разрешено деление на 0.
2005.11 Переполнение буфера в отладочном режиме при умножении двух длинных (больше 480 слов) отрицательных чисел со старшими словами 0x80000000.
Наибольшее число ошибок — 11 было обнаружено при контроле
индекса. Если его отключить, то ошибки 1-5 и 11 никак себя не проявят, т.к. они
полностью компенсируются по методу резервного элемента (примером может служить
обсуждаемая выше ошибка деления). Ошибки
Как мы сейчас увидим, большая часть арифметических ошибок миновала встроенный контроль класса. Это объясняется тем, что контроль, за исключением проверки знака, неспецифичен для ошибок арифметического типа (зато он хорошо находит фатальные и скрытые ошибки). В результате, при тестировании набралось 10 миновавших контроль ошибок, и все они оказались арифметическими. В зависимости от способа обнаружения, эти ошибки разделены на группы A, B, C:
4 ошибки группы A обнаружены при автоматической проверке результата:
2003.A1-2 Ошибки при делении отрицательного числа
2003.A3 Возведение в степень по модулю, если показатель больше модуля.
2007.A4 Возможна потеря старшего слова при умножении отрицательного и положительного числа по методу Карацубы.
3 ошибки группы B выявлены бета-тестерами класса:
2005.B1 Возведение в степень по модулю выдает 1, если старшее слово модуля равно 0
2005.B2 Пропущено число в таблице факторизации Prime.cpp.
2005.B3 Функция b_SPRP возвращает "возможно, простое" для четных чисел.
3 ошибки группы C обнаружены при повторном анализе кода класса:
2005.C1 Возведение в степень по модулю для отрицательной базы.
2005.C2 Извлечение квадратного корня из чисел размером более INT_MAX бит.
2005.C3 Комбинированный метод setneg не обращает знак числа LONG_MIN.
Уточним, что при формировании группы C мы ограничились явными ошибками, но не учитывали все случаи несоблюдения внутренних соглашений класса, например, требования нормализации чисел, т.к. они устранялись в рабочем порядке и не всегда протоколировались.
6.4. Выводы по
результатам тестирования
Все обнаруженные ошибки были устранены. Их общее число (22) мы условно принимаем за 100%, потому что не знаем, сколько ошибок еще остается в классе. При этом допущении, эффективность встроенных средств контроля и коррекции ошибок составила ~55% (12 из 22). Общая эффективность автоматических методов выявления ошибок, с учетом ошибок группы A составила ~73% (16 из 22). Ошибки группы B выявлены в модулях, для которых в то время еще не было организовано автоматическое тестирование, а иначе ошибки 2005.B1 и, возможно, 2005.B2 попали бы в группу A. По той же причине не была обнаружена автоматически ошибка 2005.C1.
Концентрация обнаруженных ошибок составила ~3 ошибки на 1000 строк комментированного кода, что много меньше известного значения в 10-50 ошибок на 1000 строк [12]. Эта разница отчасти связана с тем, что мы не учитываем все мелкие погрешности против внутренних соглашений. Кроме того, класс не тестировался на переполнение разрядной сетки. В любом случае, малая концентрация ошибок – это довод в пользу системного подхода к поиску ошибок [13], сочетающего различные методы верификации и тестирования.
Судя по распределению обнаруженных нами ошибок, базовые арифметические операции были отлажены в 2003 году, возведение в степень по модулю и проверка на простоту — в 2005 году, умножение по методу Карацубы – после его реализации в 2007 году. Критерием отлаженности считается отсутствие вновь обнаруживаемых ошибок. Этот критерий не говорит о том, что ошибок больше нет, а только о том, что поток ошибок прекратился. Поэтому интересным представляется вопрос о том, сколько ошибок еще может оставаться в классе.
6.5. Прогноз числа оставшихся ошибок
Распределение обнаруженных ошибок по годам 2003 — 2005 — 2007 составило 11 — 9 — 2. Эту тенденцию можно грубо аппроксимировать экспоненциальным распределением:
err(y) = 14.6 e y— 2003, где y — год
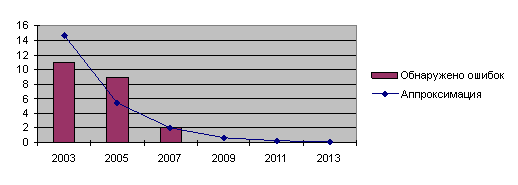
Распределение
дает 20 обнаруженных ошибок за 2003 и 2005 год, 2 ошибки за 2007 год и 1.15 вероятные ошибки, начиная с
2009 года (вычисления проводятся для двухлетних периодов). По данным нашего
тестирования, 11 ошибок из 22 являются арифметическими и 3 – потенциально
арифметическими, поэтому оценка числа ожидаемых арифметических ошибок
составляет 1.15 * (11 + 3) / 22 = 0.73. Отметим, что эта оценка дается только
для тех ошибок, которые обнаруживаются нашими программами тестирования.
7. Перспективы
автоматической верификации класса cBigNumber
Мы хотели бы полностью избавиться от ошибок в арифметическом классе, но не можем это сделать в рамках современного неформального подхода к программированию. В противовес неформальному подходу, предлагается создавать программы с применением аппарата математической логики [14-16]. Для написания программы автор должен доказать теорему об ее корректности, при этом исполняемый файл порождается транслятором только после того, как он (транслятор, а не человек) проверит доказательство. Если же доказательство будет найдено неверным, то исполняемый файл программы не будет построен.
Можно предположить, что подобная технология неимоверно усложнит программирование, но это не обязательно так. Требуется, чтобы алгоритм имел формальное математическое, а не эмпирическое обоснование. Кроме того, надо сократить число исключительных ситуаций и ветвлений. Вернемся к примеру 2 — в этой программе перемножения матриц все массивы имеют неограниченный размер и никогда не возникает переполнение разрядной сетки. Это значительно упрощает процесс доказательного программирования. А иначе транслятор может резонно спросить — почему вы уверены в том, что 2,000,000x2,000,000=4,000,000,000,000?
Внутри класса cBigNumber, к сожалению, не все так просто. Как мы увидели в двух предыдущих разделах, там могут происходить переполнения разрядной сетки и ошибки распределения памяти, невозможность которых надо доказывать формальными методами. Кроме того, класс cBigNumber создан по смешанной технологии «функции C в оболочке С++». Поэтому простые спецификации существуют только на верхних уровнях, а внутри находится множество «казуальных» функций, созданных в процессе последовательной декомпозиции задачи. Соглашения этих функций зачастую слишком сложны для проверки формальными методами. По нашей оценке, только 20% кода класса cBigNumber отвечает требованиям формальной верификации, а остальные 80% кода надо основательно переработать. Результатом переработки должна стать тщательно продуманная иерархия классов с предельно простыми соглашениями на каждом уровне и минимумом низкоуровневого кода. Такая иерархия создается естественным образом, если класс изначально создается на языке доказательного программирования. Что же касается применяемого нами C++, то этот «технарский» язык располагает к смешанной процедурно-объектной манере программирования, которая весьма далека от математической строгости формальных методов.
8. Проверка результата по методам обратной и альтернативной операции
Отказавшись от формальной верификации, мы вынуждены согласиться с тем, что математическое ядро класса может совершать ошибки. Поэтому после выполнения каждой операции следует предусмотреть проверку результата. Проверка может проводиться по классическим методам: 1) обратной операции, если таковая существует и 2) альтернативной прямой операции, если операция реализована несколькими различными способами — в этом случае можно выполнить вычисления по двум ветками и сравнить их результаты. При обнаружении несовпадения программа аварийно завершит работу, т.е. арифметическая ошибка переведется в категорию фатальных ошибок. А если фатальные ошибки недопустимы, то можно повторить расчет по третьему методу, который будет играть роль «арбитра».
Проверка будет эффективной, если проверочная операция реализует отличный от основной операции метод вычислений. Тогда вероятность двойной арифметической ошибки становится пренебрежимо малой, благодаря чему и появляется достойная альтернатива методу формальной верификации программ. Можно ожидать, что реализация проверки будет менее дорогим удовольствием по сравнению с разработкой безошибочной программы формальными методами. А еще проверка результата хороша тем, что она «отлавливает» аппаратные ошибки, возможность которых мы тоже обязаны учитывать (см. раздел 1).
Кратко опишем методику проверки операций, применяемую в программе Arifexp.
1. Сложение и вычитание нельзя проверить по методу обратной операции, т.к. эти операции реализуются по одному и тому же методу, что делает вероятной двойную ошибку. Поэтому мы основываем проверку на том, что аддитивные операции реализованы в классе двумя различными способами. Бинарные операции + и – реализованы машинно-независимым способом с помощью битовых масок, а операции накопления += и –= реализованы с помощью аппаратных операций сложения с переносом и вычитания с займом (на тех платформах, где данные аппаратные операции недоступны, они имитируются с помощью битовых масок). Различаются и внутренние способы выделения памяти — трехместный способ для бинарных операций и двуместный способ для операций накопления, с формированием результата на месте первого операнда. Наличие двух независимых реализаций позволяет выполнить проверку по методу альтернативной операции:
c = a; c += b;
if (c != a + b) throw error;
2. Умножение проверяется обратным делением. Эти алгоритмы различаются во всех отношениях, в том числе и по способу выделения памяти — он сложнее в умножении, т.к. оно основано на методе Карацубы, предусматривающем рекурсивное деление чисел на блоки.
c = a * b;
if (c / b != a) throw error;
Кроме умножения Карацубы, в классе cBigNumber есть методы умножения с таблицей сдвигов addmultab и submultab, которые не делят числа на блоки. Этими более простыми и медленными методами можно повторить умножение при обнаружении ошибки:
c = a * b;
if (c / b != a) { c = 0; if (b >= 0) c.addmultab (a.tab(), b);
else c.submultab
(a.tab(), -b); }
3. Деление проводится с остатком с помощью специального метода setdivmod и проверяется обратным умножением:
c.setdivmod
(r
= a,
b);
r += c * b;
if (r != a) throw error;
4. Квадратный корень извлекается с остатком с помощью специального метода setsqrtrm и проверяется возведением в квадрат:
c.setsqrtrm (r = a);
r += c * c;
if (r != a) throw error;
5. Возведение в степень по модулю при малом основании проверяется возведением в степень и делением на модуль.
c = cBigPowMod (a, b, m);
if (a.bits() * b < 0xFFFFFF && m != 0
&& c != cBigPow (a, b) / m) throw error;
Обе операции возведения в степень реализованы сходным образом. Проверка обнаруживает ошибки потому, что значения внутренних переменных отличаются друг от друга. Но с точки зрения эффективности и затрат времени, лучше организовать проверку каждой внутренней операции умножения и деления.
Проверка деления и квадратного корня не приводит к заметным накладным расходам, т.к. выполняется на порядок более быстрой операцией умножения. Сложнее обстоит дело с операциями сложения/вычитания и умножения — все доступные в классе cBigNumber проверочные методы намного медленнее основного метода. Здесь лучшим решением может быть применение альтернативного вычислительного пакета, такого как обсуждавшиеся выше пакеты GMP и NTL.
Отметим также, что проверка может выполняться в дополнительных не синхронизированных потоках параллельно с выполнением основных вычислений – это пригодится на многопроцессорных и многоядерных системах, когда они будут в достаточной степени отлажены.
Заключение
Специфика расчетных программ такова, что мы ждем от них
математической точности вычислений. Но математической строгостью обладают
только методы решения задач, а технология их программирования еще не доведена
до этого высокого уровня. Расчетные программы могут ошибаться, поэтому при их
выборе надо обратить внимание на статистику ошибок, а также использование авторами
программ автоматических методов отладки и тестирования, которые в несколько раз
эффективнее ручных методов.
Дополнительными и непредсказуемыми источниками ошибок являются транслятор и аппаратное вычислительное устройство. Поэтому желательно использовать тот же транслятор и вид микропроцессора, что применяли при тестировании авторы программы. И что само собой разумеется – необходимо перепроверять результаты расчетов с применением альтернативных методов.
Класс cBigNumber,
в зависимости от размерности задачи, подойдет на роль основного расчетного или
проверочного средства. Класс прост в использовании и обладает высокой производительностью
на платформе Windows
благодаря применению встроенного ассемблера. Сильные стороны класса – простые
алгоритмы, использование наиболее надежных аппаратных средств и повышенная
достоверность результатов вычислений.
Реализация класса, тестовые программы и инструкции по применению доступны для загрузки со страницы http://www.imach.uran.ru/cbignum
Литература
1.
Prime95
download page: http://www.mersenne.org/freesoft.htm
2. Крис Касперски. Дефекты проектирования Intel Core 2 Duo Системный администратор 6(67) июнь 2008 с. 50-59. http://www.samag.ru/cgi-bin/go.pl?q=articles;n=06.2008;a=01
3.
The
GNU MP Bignum Library: http://www.swox.com/gmp/
4.
GMP
Install Instruction for Windows Platform: http://www.cs.nyu.edu/exact/core/gmp/
5. Дональд Э. Кнут. Искусство программирования, том 2. Насколько быстро можно выпол-нять умножение.
6.
A
Library for doing Number Theory: http://www.shoup.net/ntl/
7.
Р.Н.Шакиров. Oценка эффективности динамических
массивов с автоматической провер-кой индекса // Новые
информационные технологии в исследовании сложных структур: Докл.
III Всеросс.
конф. с межд. участием. Томск, 10-12 сентября 2002.
С.383-388.
http://www.imach.uran.ru/exarray/papers/exarrayp.htm
8.
Р.Н.Шакиров. Шаблоны для организации контроля индексов
в программах на языках С++ и С // IEEE AIS'03 CAD-2003: Труды. Дивноморское,
3-10 сентября 2003. Т.2, С.191-207.
http://www.imach.uran.ru/exarray/papers/ex2003p.htm
9.
Р.Н.Шакиров.
Принципы разработки межплатформенного класса cBigNumber для реали-зации арифметических операций над целыми
числами неограниченной разрядности // Компьютерная безопасность и криптография:
Докл. 4 сибирской научной школы-семинара с межд.
участием SIBERCRYPT'05.
Томск, 6-9 сентября 2005.
http://www.imach.uran.ru/cbignum/papers/cb2005p.htm
10.
Е.С.Чернов, В.В.Кулямин
Тестирование современных библиотек тригонометрических функций // Подход UniTESK: итоги и перспективы. Труды ИСП
РАН, 14(1). 2008. С. 163-179.
11.
Miller
strong probable prime test: http://www.utm.edu/research/primes/prove/prove2_3.html
12. C. Макконнелл. Совершенный код. М.: Русская редакция, 2005.
13. В.В.Кулямин. Перспективы интеграции методов верификации программного обеспечения. 2009. http://www.citforum.ru/SE/testing/integration/
14. В.В.Кулямин. Методы верификации программного обеспечения.
Всероссийский конкурс обзорно-аналитических статей по приоритетному направлению
"Информационно-телекоммуникационные системы", 2008. 117c.
http://window.edu.ru/window/library?p_rid=56168
15. Роберт Лоренс Бейбер. Программное обеспечение без ошибок. M.: Радио и связь, 1996. 176с.
16. В.А.Непомнящий, О.М.Рякин. Прикладные методы верификации программ. М.: Радио и связь, 1988. 256c.